이진 탐색 알고리즘
오름차순 정렬되어 있는 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 방법이다.
이진 탐색은 시작점, 끝점, 중간점을 이용하여 탐색 범위를 설정한다.
시간 복잡도: O(logN)
동작 과정
0) 오름차순 정렬된 데이터에서 값이 '4'인 원소 찾기

1) 시작점: 0, 끝점: 9, 중간점: 4 (소수점 이하 제거)
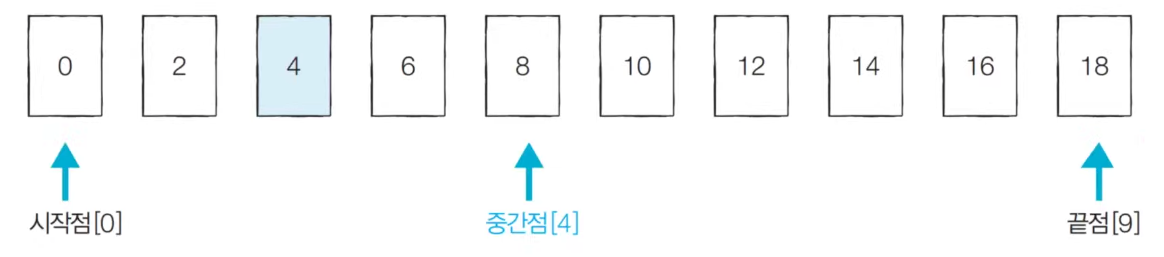
2) 중간점보다 4가 작으므로 시작점: 0, 끝점: 3, 중간점: 1
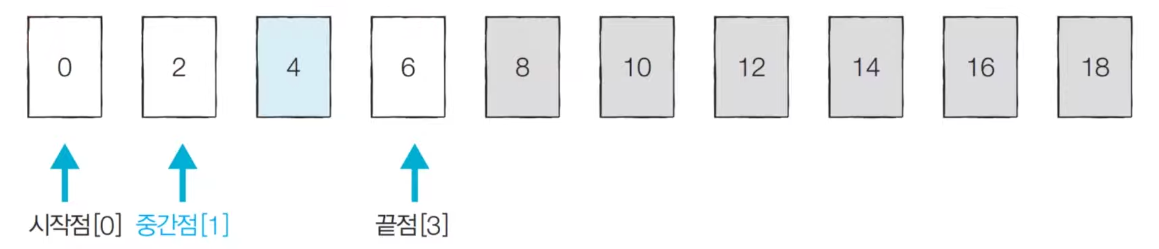
3) 중간점보다 4가 크므로 시작점: 2, 끝점: 3, 중간점: 2

예제코드
반복
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// 원소의 개수(n)와 찾고자 하는 값(target)을 입력받기
int n = sc.nextInt();
int target = sc.nextInt();
// 전체 원소 입력받기
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = sc.nextInt();
}
// 이진 탐색 수행 결과 출력
int result = binarySearch(arr, target, 0, n - 1);
if (result == -1) {
System.out.println("원소가 존재하지 않습니다.");
} else {
System.out.println(result + 1);
}
}
// 이진 탐색 소스코드 구현
public static int binarySearch(int[] arr, int target, int start, int end) {
while (start <= end) {
// 중간점 찾기
int mid = (start + end) / 2;
if (arr[mid] == target) { // 찾은 경우 중간점 인덱스 반환
return mid;
} else if (arr[mid] > target) { // 중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽 확인
end = mid - 1;
} else {
start = mid + 1; // 중간점의 값보다 찾고자 하는 값이 큰 경우 오른쪽 확인
}
}
return -1;
}
}
재귀
public static int binarySearch(int[] arr, int target, int start, int end) {
if (start > end) return -1;
int mid = (start + end) / 2;
// 찾은 경우 중간점 인덱스 반환
if (arr[mid] == target) {
return mid;
} else if (arr[mid] > target) {
// 중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽 확인
return binarySearch(arr, target, start, mid - 1);
} else {
// 중간점의 값보다 찾고자 하는 값이 큰 경우 오른쪽 확인
return binarySearch(arr, target, mid + 1, end);
}
}'알고리즘 개념정리' 카테고리의 다른 글
| 퀵 정렬 (0) | 2022.08.01 |
|---|---|
| 삽입 정렬 (0) | 2022.08.01 |
| 선택 정렬 (0) | 2022.07.31 |
| BFS (Breadth-First Search) (0) | 2022.07.30 |
| DFS (Depth-First Search) (0) | 2022.07.30 |